I learned the concept of PCA today, and found out this method of reducing dimension is quite terse.
If we do PCA to a 40-d dataset, reduce it into a 2-d dataset, it simply choose the 2 most “Principal Components”, i.e. the 2 most “important” dimensions, and drop others.
So, before we do PCA, we’d better do a scree of PCA, to plot the proportion of variance of each dimension.
take a look at this implementation.
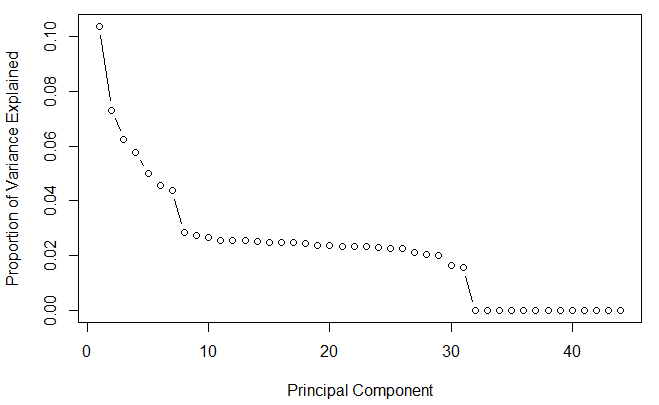
In this example, I think we are quite safe to simply drop dimensions after PC30, i.e. we can use PCA to reduce the dataset to 30-d quite safely. (and then we may use t-sne, a more time-consuming method.)